As we know volatile velocity from surface of a celestial body is given by following equation:
Where V is volatile velocity of the bullet, M is mass of heavy celestial body, G is constant of global gravity, and r is distance of center of heavy mass from center of the bullet. In classic physics, kinetic energy of a bullet will be calculated by the following equation:
Where E is kinetic energy and m is mass of a bullet. Now, we want to calculate kinetic energy of the material in volatile velocity:
Where U is classic gravity potential energy. The gained result is classic gravity potential energy, because the volatile velocity is given by the following equation:
Now, we calculate relative gravity potential energy of the bullet:
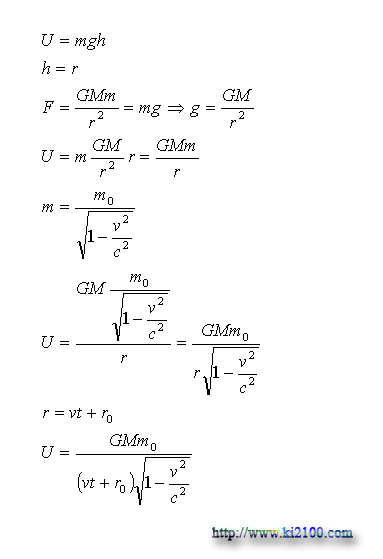
Where g is gravity acceleration, h is height or distance of gravity field center and center of bullet, i.e. r, F is gravity between celestial body and bulle, m0 is tranquility mass of bullet, C is the light velocity, and r0 is primary distance of celestial body and bullet. In other hand, we have:
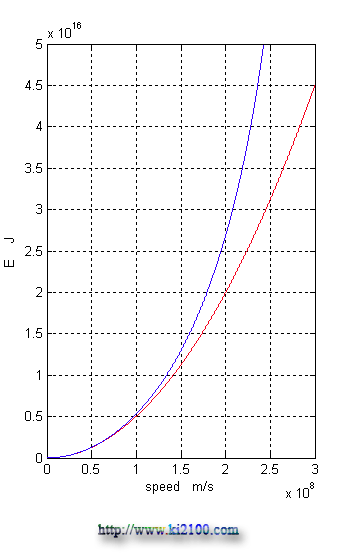
Comparison Diagram of Classic Kinetic Energy and Relative Kinetic Energy
The bottom curve indicates increasing classic kinetic energy and the upper curve indicates increasing relative kinetic energy of the bullet. In order to calculate volatile velocity, by comparison relative kinetic energy and relative potential energy of the bullet, we have:
There is gained the same previous result in classic physics. So, this equation is validated in relativity (high velocities). Now we draw and comparison diagrams of classic gravity potential energy and relativity gravity potential energy. We consider the motion as accelerated motion and its accelerate is supposed as C in square of second, i.e. by supposing a=c, we have:
Where d is covered distance, and a is acceleration.
By considering to this matter that the above equation is always a constant numerical, in comparison with time, velocity, and acceleration of bullet, by displacing 10^7 instead GMm0, we can draw curves.
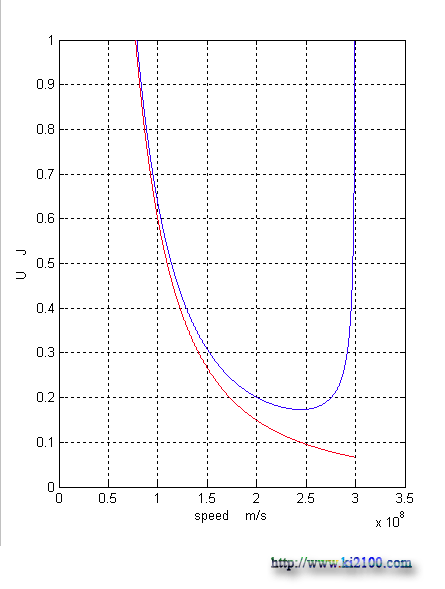
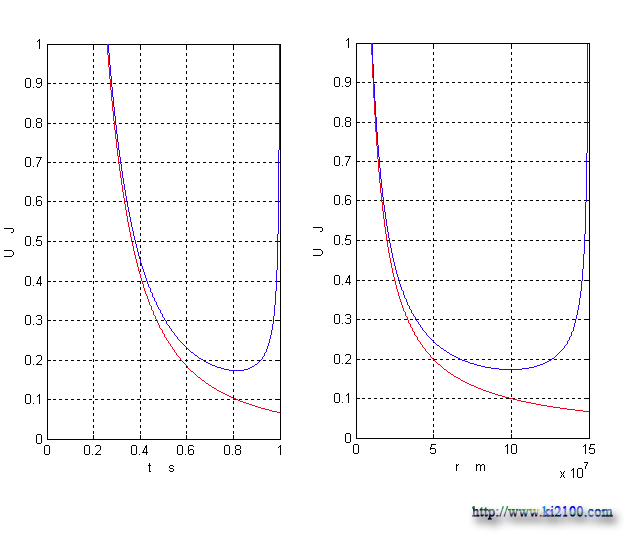
The bottom curve is related to classic gravity potential energy of bullet, but the upper curve indicates its relativity gravity potential energy. It is clear that relativity gravity potential energy is decreased to 250.000 Km/s, but it is increased after that.Now, we draw diagrams according to time and distance:
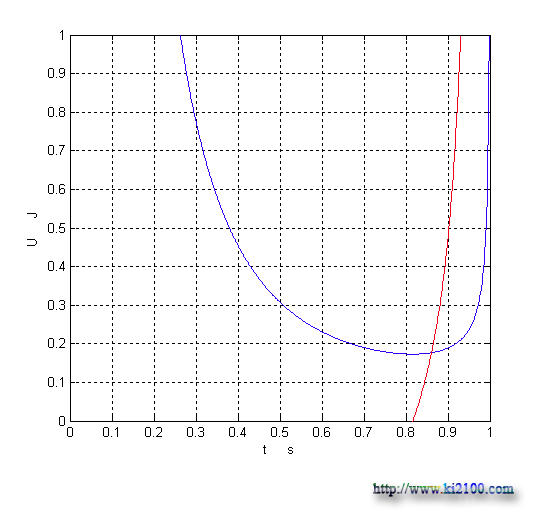
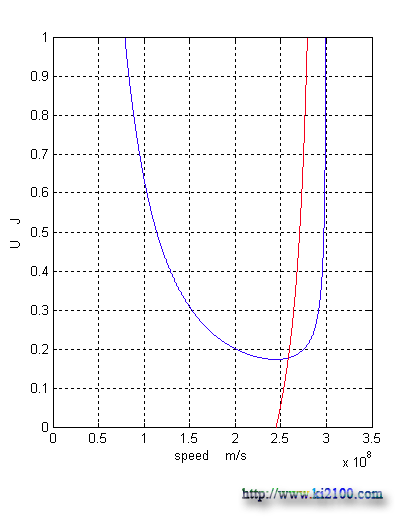
As you see in the above diagrams, diagrams of relativity gravity potential energy have a minimum quantity comparison with time, velocity, and distance. In order to find this quantity, we must calculate differential of resulted equation or function for relativity gravity potential energy according to time, and consider it as zero and then calculate time:
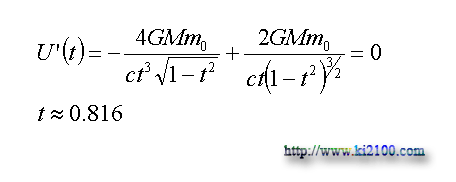
This quantity has been gained for time approximately and by drawing differential diagram (the following vertical curve):
And for this velocity, we certainly have:
Which it is gained 245,000 Km/s. By considering to these matters, we can calculate our depth vision in cosmos.
Our depth vision in cosmos:
As we said previously, Big Bang Theory is an impossible theory. Now, if we suppose that energy and particles could escape from primary hot corpuscle, acceleration of the cosmos expansion could not be more than c/s^2, and resulted equation about relativity gravity potential energy is considered in this topic. As you can see in the above diagrams, relativity gravity potential energy of escaped masses with acceleration c/s^2 in velocity 245.000 Km/s is a minimum energy, but it will be increased after that; it seems that increasing velocity will be stopped in this point and therefore, velocity is constant and acceleration will be zero, because in order to increase velocity, we need a huge kinetic energy, which its providing source is uncovered yet. As we know observations of Hobble, a great physicist, showed that galaxies are being far from us by V velocity, which it is resulted by the following equation:
V=HXWhere H is Hobble constant, and X is distance from the Earth. In fact, this equation can be used for any point of the world. In briefly, velocity will be increased about 20 Km/s, instead of each one million light year distance from us. The farthest distance of celestial bodies from us is estimated 12 billion light years, i.e. sent ultra-depth picture by mapping camera of Hobble, NASA. Now, by considering to the above – mentioned matters, we can calculate our depth vision in cosmos. For this, we divide volatile velocity 245.000 Km (the maximum current volatile velocity in the cosmos, resulted from Big Bang theory and relativity theory) on 20 Km/s, which we get 12.25 billion light year, and it is supposed that there isn’t anything upper than this permitted velocity! But in future, if celestial bodies will be observed beyond our current depth vision, which they have certainly more distance and velocity, Big Bang Theory will be cancelled in explanation of the cosmos extension spontaneously.
Author: Mohammadreza Tabatabaei
June 9, 2009
http://ki2100.com/english/physics/cosmology/E_U_r.htm
دوست عزیز، به سایت علمی نخبگان جوان خوش آمدید
مشاهده این پیام به این معنی است که شما در سایت عضو نیستید، لطفا در صورت تمایل جهت عضویت در سایت علمی نخبگان جوان اینجا کلیک کنید.
توجه داشته باشید، در صورتی که عضو سایت نباشید نمی توانید از تمامی امکانات و خدمات سایت استفاده کنید.



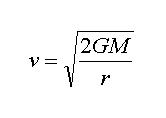
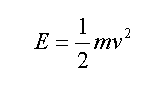
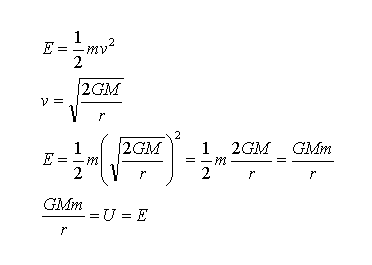
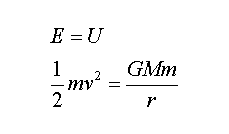
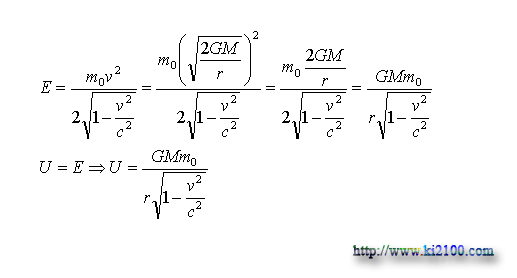
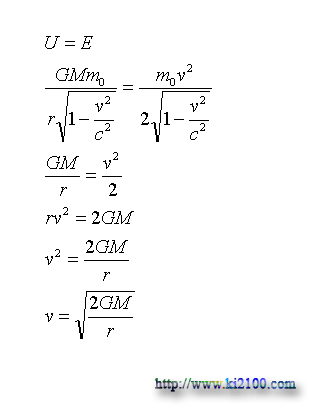
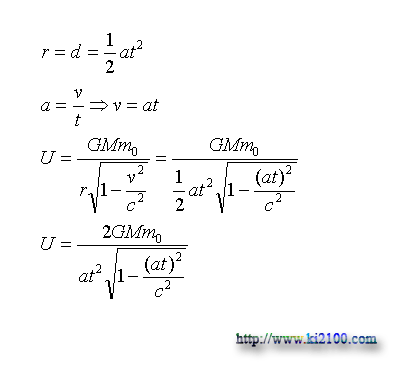
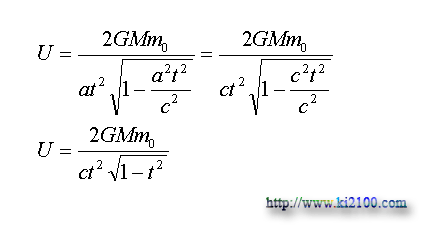




 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (Bookmarks)