كند شدن زمان و كوتاه شدن متر در ميدان گرانشي ، انتقال به آبي يا سرخ گرانشيطرح ايراد دوم در نظريه نسبيت عامهمانطور كه در مبحث نظريه انفجار بزرگ محال است توضيح داده شد ، سرعت فرار از سطح يك جرم سماوي ثقيل از رابطه زير بدست ميآيد :
v سرعت فرار پرتابه ، M جرم جسم سماوي ، G ثابت جهاني گرانش و r فاصله مركز جسم ثقيل تا مركز پرتابه است . اينك اگر سرعت فرار را سرعت نور فرض كنيم ، شعاع شوارتس شيلد بدست ميآيد . يعني كمتر از اين فاصله از مركز جرم سماوي همانند يك سياه چاله ، نور توان فرار و خروج را نخواهد داشت و در نهايت جذب سياه چاله خواهد شد . برعكس اين موضوع نيز صادق است ، يعني اگر جسمي به طرف سياه چاله سقوط كند ، چنين به نظر ميرسد كه در اين شعاع يا فاصله از مركز سياه چاله ( شعاع شوارتس شيلد ) ، سرعت سقوط جسم به سرعت نور نزديك شود و در اين شرايط ، زمان براي آن تقريبا متوقف و طول نيز تقريبا صفر خواهد شد و به اين مكان به اصطلاح نقطه صفر فضا - زمان اطلاق ميشود . و اين مكان ويژه ميتواند مبدا مناسبي براي محاسبه و اندازه گيري تاثيرات گرانش بر زمان و متر ( فضا - زمان ) باشد . براي اينكار سرعت فرار پرتابه را به جاي سرعت جسم در معادلات زير مربوط به تغييرات زمان و متر ارايه شده توسط لورنتس و جرالد قرار ميدهيم :
t زمان ، 't زمان كند شده ، c سرعت نور ، d طول و 'd طول كوتاه شده است . دو معادله بدست آمده فوق ، معادلات كلي براي بدست آوردن تغييرات ايجاد شده در طول و زمان در يك ميدان گرانشي ميباشد . بنابراين طبق تعريف خواهيم داشت :
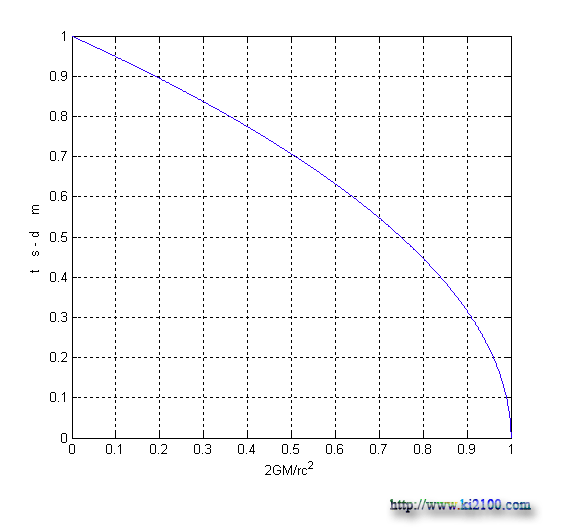
نمودار افزايش شدت ميدان گرانشي و كند شدن زمان و كوتاه شدن متر
با توجه به اينكه حركت و سرعت نور وابسته به فضا - زمان پيرامون ( محيط ) است و همواره تحت هر شرايطي ثابت اندازه گيري ميشود ، طول موج نور نيز ميبايست به نسبت كوتاه شدن متر ، كوتاه شود يعني :
معادله فوق در زمان سقوط نور به ميدان گرانشي صادق است ولي در زمان فرار نور از ميدان گرانشي ، معادله زير حاكم خواهد بود :
يعني درست عكس حالت قبل . λ طول موج و 'λ طول موج كوتاه يا بلند شده است .
نمودار سقوط و يا فرار نور و تغيير طول موج آن ( انتقال به آبي يا انتقال به سرخ گرانشي )با توجه به اينكه معادلات زير تحت هر شرايطي همواره برقرار هستند :
f فركانس ( بسامد ) و 'f فركانس تغيير يافته است ، پس نتيجه ميشود :
معادله فوق در زمان سقوط نور به ميدان گرانشي صادق است ولي در زمان فرار نور از ميدان گرانشي معادله زير حاكم خواهد بود :
يعني درست عكس حالت قبل . اين دو ، پديدهاي هستند كه به آنها انتقال به سرخ گرانش و يا انتقال به آبي گرانش گفته ميشود .
نمودار سقوط و يا فرار نور و تغيير فركانس آن ( انتقال به آبي يا انتقال به سرخ گرانشي )
در حقيقت سرعت فرار در اين مكان سرعت نور است . يعني طول موج به طرف صفر و فركانس موج به طرف بي نهايت حركت ميكند و همچنين زمان و متر ( فضا - زمان ) به صفر ميل ميكند .
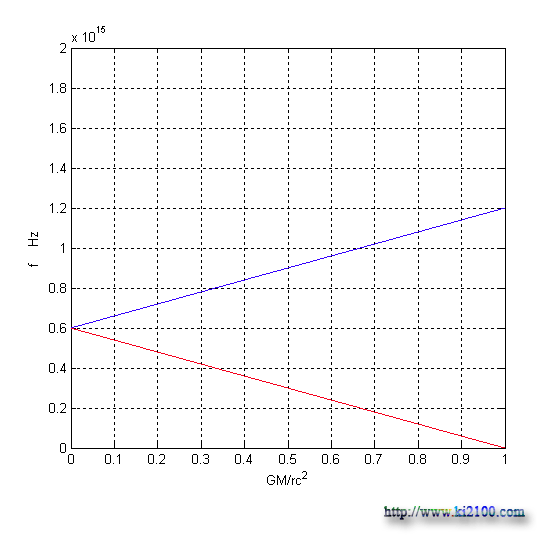
جالب است بدانيم كه نسبيت در مورد كند شدن زمان و كوتاه شدن متر همان معادلات ارايه شده در اين مبحث را پيشنهاد ميكند ولي در مورد تغيير فركانس ، معادله زير را پيشنهاد كرده است :
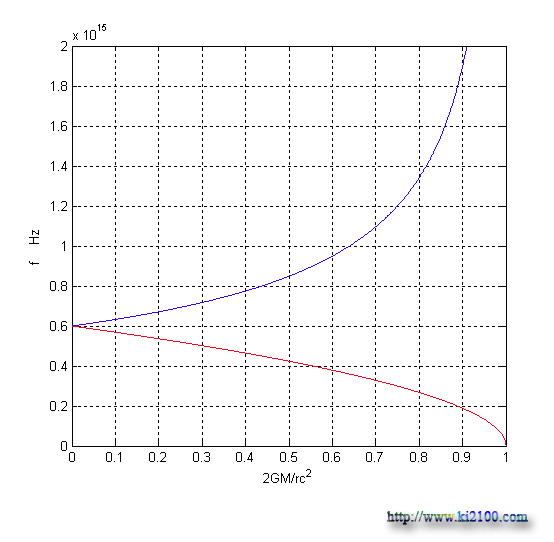
اينك نمودار معادله فوق را رسم ميكنيم :
معادله وضع شده در نسبيت عام دو ايراد و مشكل جدي دارد :
1- نمودار به جاي اينكه منحني باشد ، خطي است .
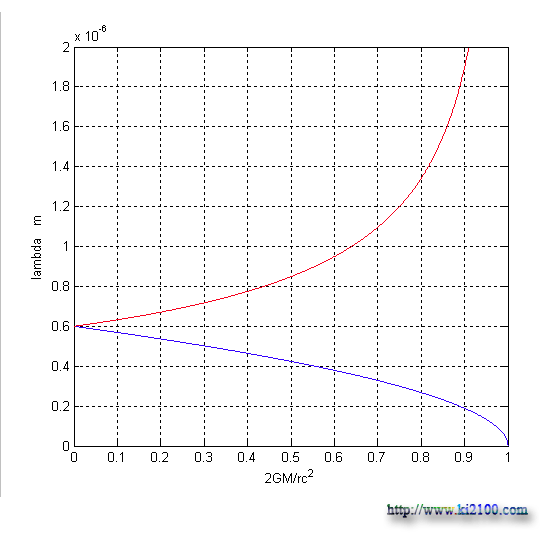
2- معادله در قسمت فرار نور از شعاع شوارتس شيلد ( به كار بردن علامت منفي ) درست به نظر ميرسد ، چون فركانس نور صفر شده و نور از حركت باز ميايستد . ولي در قسمت سقوط نور به ميدان گرانش ( استفاده از علامت مثبت ) فركانس نور در نهايت دو برابر ميشود و بيشتر از آن ممكن نيست كه مقدار بسيار كم و ناچيزي است كه انرژي و فركانس نور در زمان سقوط به طرف يك سياه چاله خيلي بيشتر از اينها خواهد بود كه با اين فرمول قابل محاسبه نيست . اينك نمودارهاي فوق را با هم ادغام ، مقايسه و برسي ميكنيم :
بسيار واضح و روشن است كه معادلات بدست آمده و ارايه شده در اين مبحث ، صحيح تر و دقيق تر از معادله ارايه شده توسط نسبيت عام انيشتين است . كه اين ايراد به نظريه نسبيت عام وارد و موجه خواهد بود .
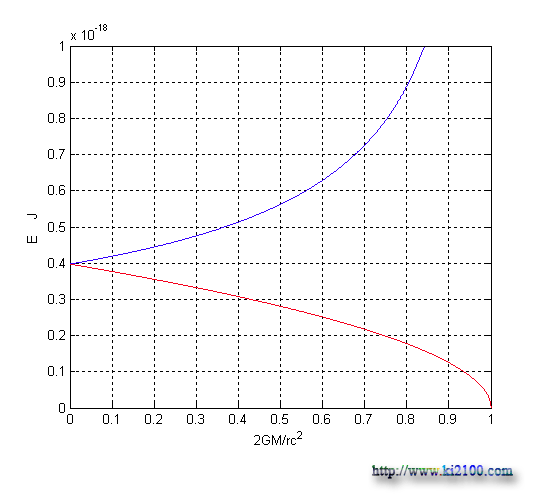
اينك انرژي موج الكترومغناطيس را در زمان سقوط به ميدان گرانشي محاسبه ميكنيم :
E انرژي كوانتوم تابش الكترومغناطيس ، 'E انرژي ثانويه و h ثابت پلانك است . معادله فوق در زمان سقوط نور به ميدان گرانشي صادق است ولي در زمان فرار نور از ميدان گرانشي معادله زير حاكم خواهد بود :
يعني درست عكس حالت قبل . اين معادلات براي اولين بار در مورد فركانس و انرژي نور در هنگام انتقال به آبي يا سرخ گرانشي مطرح ميشوند و آزمونهاي دقيق در آينده ميتواند صحت و دقت آنها را معلوم و مشخص كند .
نمودار سقوط و يا فرار نور و تغيير انرژي آن ( انتقال به آبي يا انتقال به سرخ گرانشي )
محمدرضا طباطبايي 10/3/88
منبع: http://ki2100.com/physics/gravity_time.htm
دوست عزیز، به سایت علمی نخبگان جوان خوش آمدید
مشاهده این پیام به این معنی است که شما در سایت عضو نیستید، لطفا در صورت تمایل جهت عضویت در سایت علمی نخبگان جوان اینجا کلیک کنید.
توجه داشته باشید، در صورتی که عضو سایت نباشید نمی توانید از تمامی امکانات و خدمات سایت استفاده کنید.



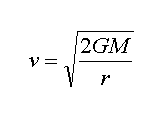
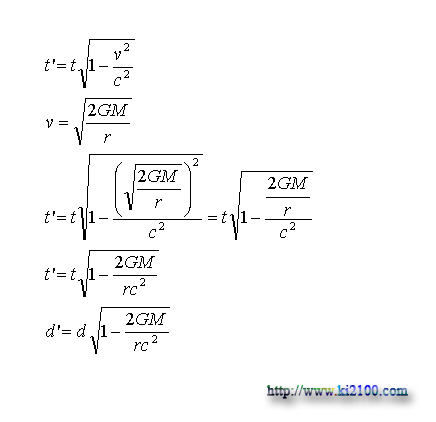
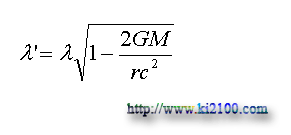
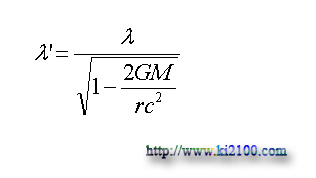
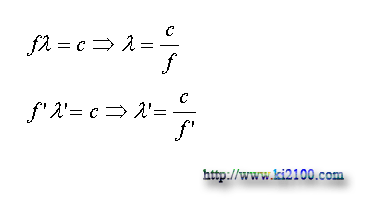
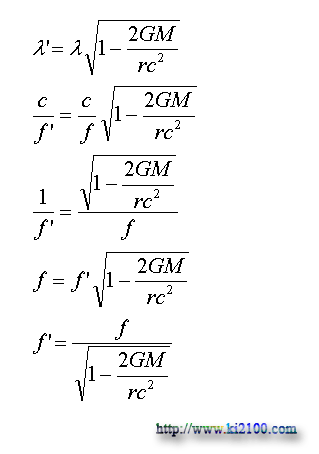
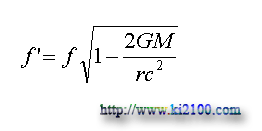
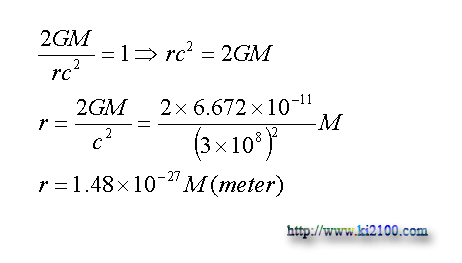
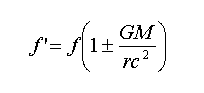

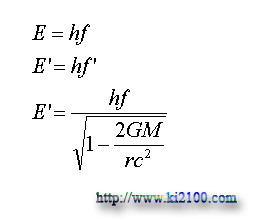



 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (Bookmarks)